Nowadays, anybody with a smartphone can find their exact position with just one click. Any location is determined by a specific pairing of latitude and longitude in a Cartesian coordinate ellipsoid-based grid.
The actual shape of the Earth is an irregular figure called a geoid but it can be approximated (at sea level) to a mathematical ellipsoid called a datum. The more recent and precise version of the global datum is the World Geodetic System WGS84 (established in 1984 and revised in 2004), although there are also some local datums such as the European ED50.
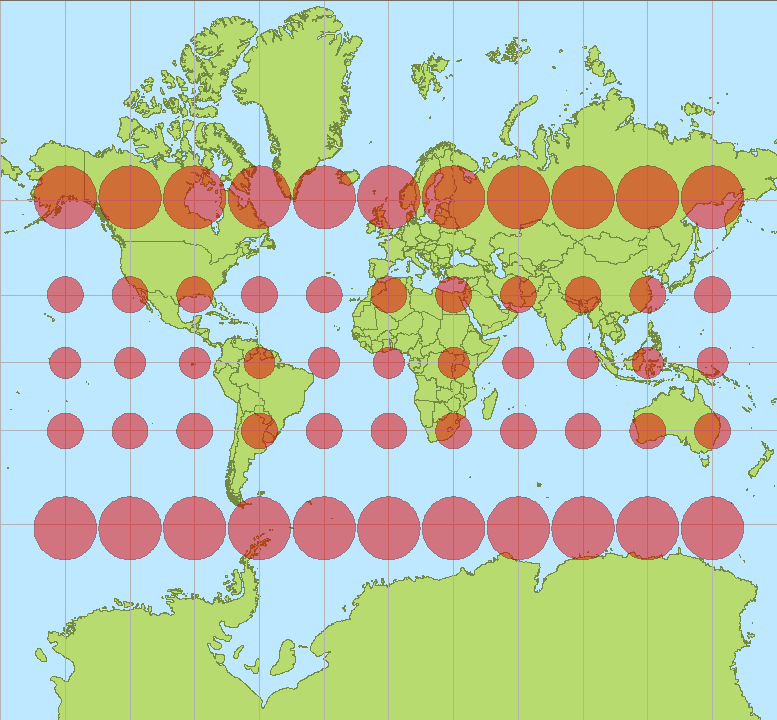
Depending on what the map is needed for, one projection may be better than another, and there are lots of different map projections that can be classified by two main criteria:
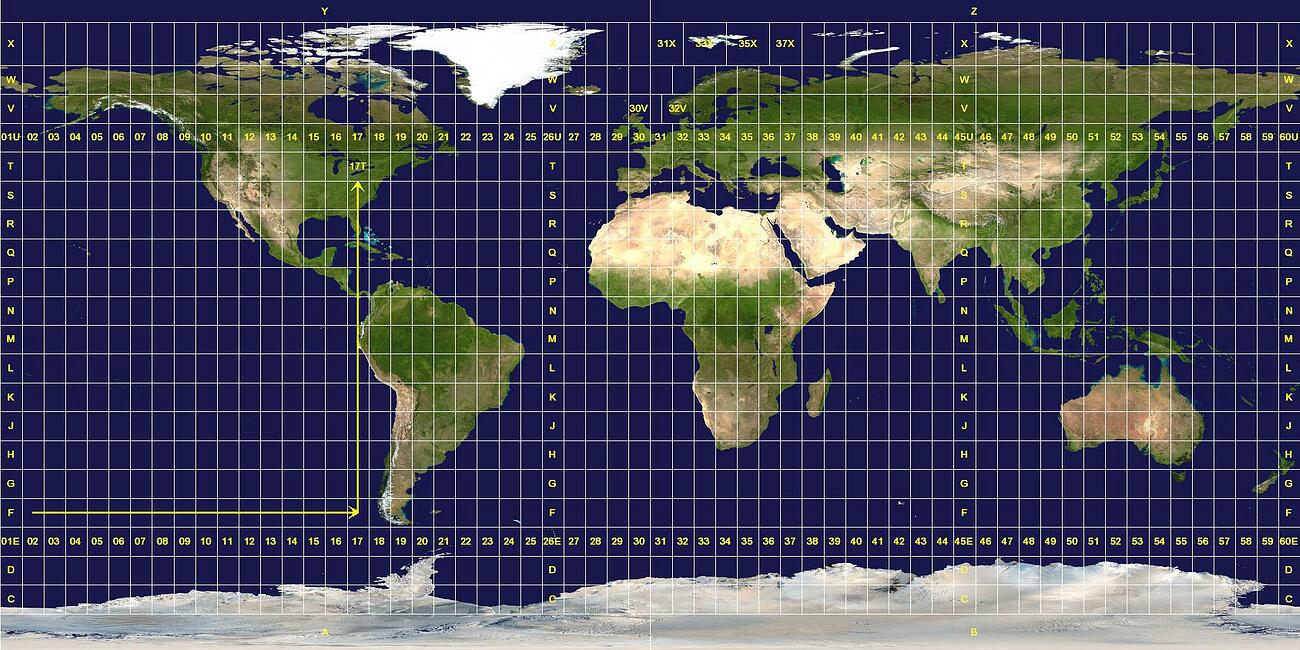
The Universal Transverse Mercator, however, is not a single map projection but a system that divides the Earth into sixty zones, each being a six-degree band of longitude (numbered from 01 to 60, west to east). These bands are divided into cells eight degrees high of latitude (specified by a letter from A to X, south to north, with N being the first letter north of the equator.)